SELINA Solutions for Class 9 Maths Chapter 25 - Complementary Angles
Chapter 25 - Complementary Angles Exercise Ex. 25

![]()
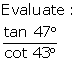
![]()

![]()
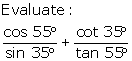
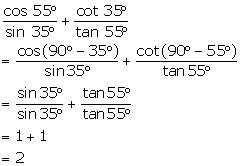
![]()

![]()
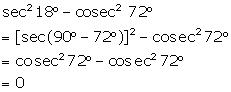
![]()

![]()

![]()

![]()
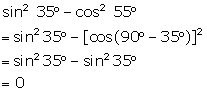
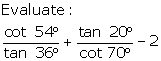
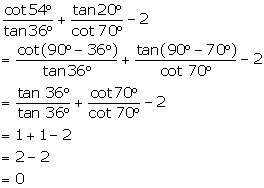
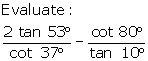

![]()
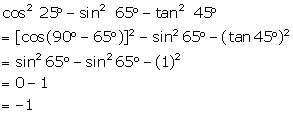
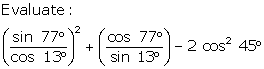
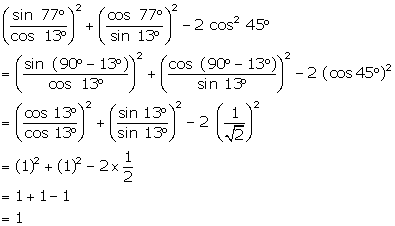
Show that:
tan 10° tan 15° tan 75° tan 80° = 1
L.H.S.
= tan 10° tan 15° tan 75° tan 80°
= tan (90° - 80°) tan (90° - 75°) tan 75° tan 80°
= cot 80° cot 75 ° tan 75° tan 80°
= (cot 80° tan 80°)(cot 75° tan 75°)
= (1)(1)
= 1
= R.H.S.
Show that:
sin 42° sec 48° + cos 42° cosec 48° = 2
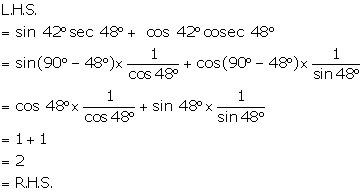
Express each of the following in terms of angles between 0°and 45°:
(i) sin 59°+ tan 63°
(ii) cosec 68°+ cot 72°
(iii)cos 74°+ sec 67°

For triangle ABC, show that:
(i) ![]()
(ii) ![]()
(i) We know that for a triangle ![]() ABC
ABC
![]() A +
A + ![]() B +
B + ![]() C = 180°
C = 180°
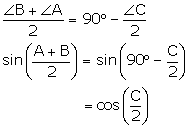
(ii) We know that for a triangle ![]() ABC
ABC
![]() A +
A + ![]() B +
B + ![]() C = 180°
C = 180°
![]() B +
B + ![]() C = 180° -
C = 180° - ![]() A
A
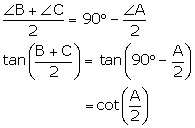
Evaluate:
(i) ![]()
![]()
(iii) ![]()
![]()
(iv) ![]()
(v) ![]()
(vi) ![]()
(vii) ![]()
(viii) ![]()
(ix) ![]()
(i)
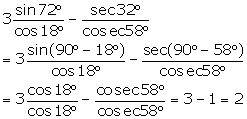

(iii) ![]()

(iv) ![]()
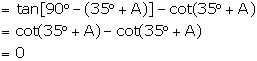
(v) ![]()
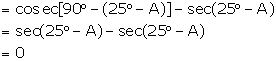
(vi) ![]()
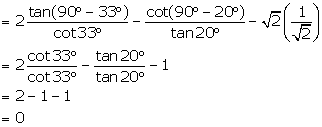
(vii) ![]()
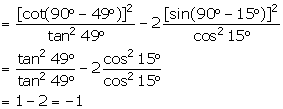
(viii) ![]()
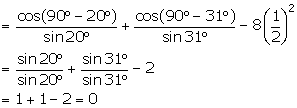
(ix) ![]()
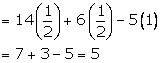
![]()

In each case, given below, find the value of angle A, where 0° ≤ A ≤ 90°.
sin (90° - 3A).cosec 42° = 1
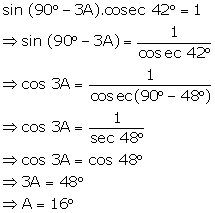
In each case, given below, find the value of angle A, where 0° ≤ A ≤ 90°.
cos (90° - A).sec 77° = 1
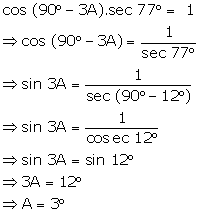
Comments
Post a Comment