SELINA Solutions for Class 9 Maths Chapter 22 - Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals]
Chapter 22 - Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals] Exercise Ex. 22(A)
From the following figure, find the values of :
(i) sin A
(ii) cos A
(iii) cot A
(iv) sec C
(v) cosec C
(vi) tan C.
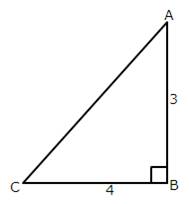
Given angle ![]()
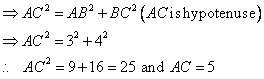
(i)
![]()
(ii)
![]()
(iii)
![]()
(iv)
![]()
(v)
![]()
(vi)
![]()
Form the following figure, find the values of :
(i) cos B
(ii) tan C
(iii) sin2B + cos2B
(iv) sin B. cos C + cos B. sin C
Given angle ![]()


(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
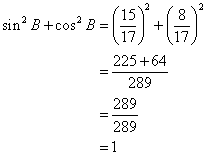
(iv)
![]()
![]()
![]()
![]()
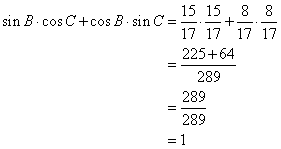
From the following figure, find the values of :
(i) cos A (ii) cosec A
(iii) tan2A - sec2A (iv) sin C
(v) sec C (vi) cot2 C - ![]()

Consider the diagram as

Given angle ![]() and
and ![]()


(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
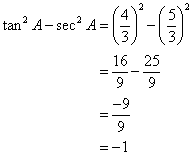
(iv)
![]()
(v)
![]()
(vi)
![]()
![]()

From the following figure, find the values of :
(i) sin B (ii) tan C
(iii) sec2 B - tan2B (iv) sin2C + cos2C

Given angle ![]() and
and ![]()



(i)
![]()
(ii)
![]()
(iii)
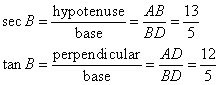
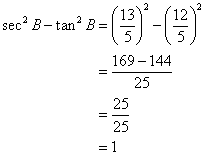
(iv)


Given: sin A = ![]() , find :
, find :
(i) tan A(ii) cos A
Consider the diagram below:
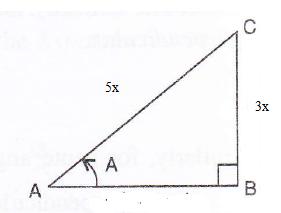
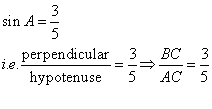
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
(i)
![]()
(ii)
![]()
From the following figure, find the values of :
(i) sin A
(ii) sec A
(iii) cos2 A + sin2A
Given angle ![]() in the figure
in the figure


Now
(i)![]()
(ii)![]()
(iii)![]()
![]()
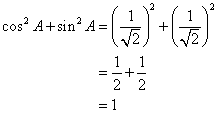
Given: cos A = ![]()
Evaluate: (i) ![]() (ii)
(ii) ![]()
Consider the diagram below:
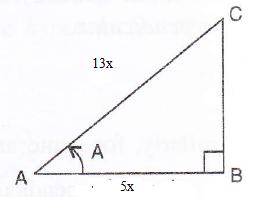
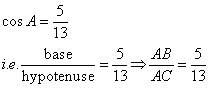
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
![]()
![]()
(i)
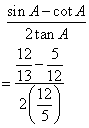

(ii)
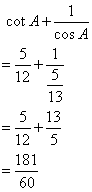
Given: sec A = ![]() , evaluate : sin A -
, evaluate : sin A - ![]()
Consider the diagram below:
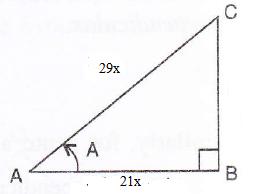
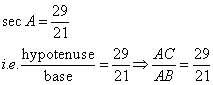
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
![]()
Therefore

Given: tan A = ![]() , find :
, find : ![]()
Consider the diagram below:
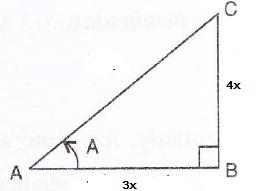
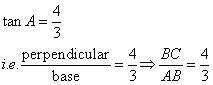
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
![]()
![]()
Therefore
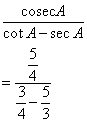
![]()
![]()
Given: 4 cot A = 3 find;
(i) sin A
(ii) sec A
(iii) cosec2 A - cot2A.
Consider the diagram below:
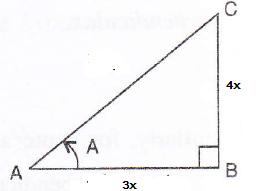
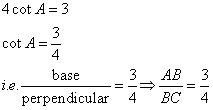
Therefore if length of AB = 3x, length of BC = 4x
Since

(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
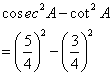
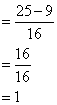
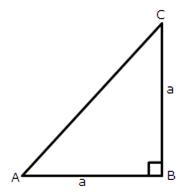
Given: cos A = 0.6; find all other trigonometrical ratios for angle A.
Consider the diagram below:
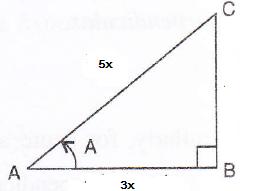
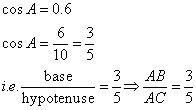
Therefore if length of AB = 3x, length of AC = 5x
Since

Now all other trigonometric ratios are
![]()
![]()
![]()
![]()
![]()
In a right-angled triangle, it is given that A is an acute angle and tan A =![]() .
.
find the value of :
(i) cos A(ii) sin A(iii) ![]()
Consider the diagram below:
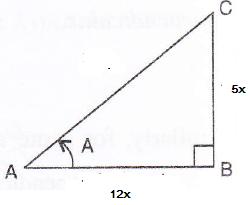
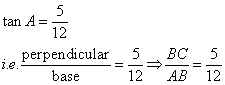
Therefore if length of AB = 12x, length of BC = 5x
Since

(i)
![]()
(ii)
![]()
(iii)
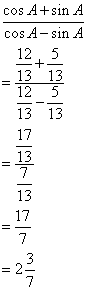
Given: sin ![]()
Find cos ![]() + sin
+ sin ![]() in terms of p and q.
in terms of p and q.
Consider the diagram below:

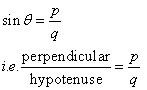
Therefore if length of perpendicular = px, length of hypotenuse = qx
Since

Now
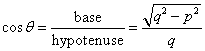
Therefore
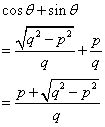
If cos A = ![]() and sin B =
and sin B = ![]() , find the value of :
, find the value of : ![]() .
.
Are angles A and B from the same triangle? Explain.
Consider the diagram below:
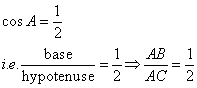
Therefore if length of AB = x, length of AC = 2x
Since

Consider the diagram below:
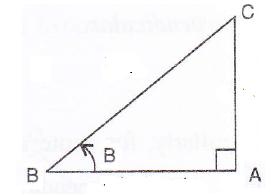
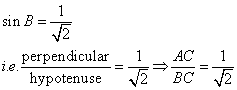
Therefore if length of AC = x, length of ![]()
Since

Now
![]()
![]()
Therefore
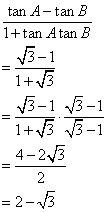
If 5 cot ![]() = 12, find the value of : Cosec
= 12, find the value of : Cosec ![]() + sec
+ sec ![]()
Consider the diagram below:
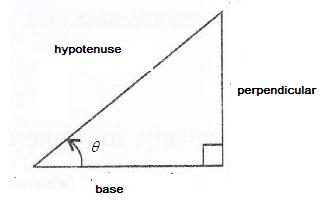
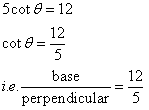
Therefore if length of base = 12x, length of perpendicular = 5x
Since

Now
![]()
![]()
Therefore
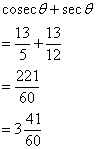
If tan x = ![]() , find the value of : 4 sin2x - 3 cos2x + 2
, find the value of : 4 sin2x - 3 cos2x + 2
Consider the diagram below:

Therefore if length of base = 3x, length of perpendicular = 4x
Since
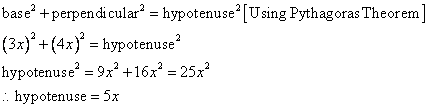
Now
![]()
![]()
Therefore
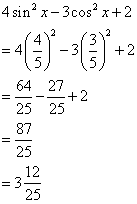
Ifcosec ![]() =
= ![]() , find the value of:
, find the value of:
(i) 2 - sin2 ![]() - cos2
- cos2 ![]()
(ii) ![]()
Consider the diagram below:
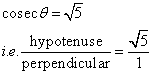
Therefore if length of hypotenuse ![]() , length of perpendicular = x
, length of perpendicular = x
Since

Now
![]()
![]()
(i)

(ii)
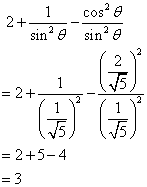
If sec A = ![]() , find the value of :
, find the value of :
![]()
Consider the diagram below:
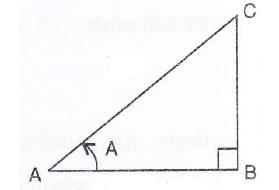
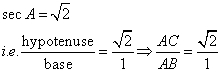
Therefore if length of AB = x, length of ![]()
Since

Now
![]()
![]()
![]()
Therefore

If cot ![]() = 1; find the value of: 5 tan2
= 1; find the value of: 5 tan2 ![]() + 2 sin2
+ 2 sin2 ![]() - 3
- 3
Consider the diagram below:
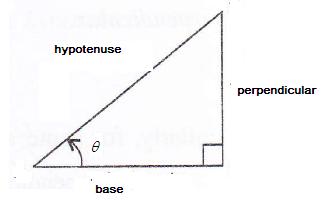
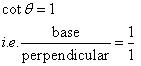
Therefore if length of base = x, length of perpendicular = x
Since
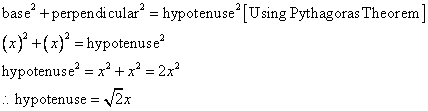
Now
![]()
![]()
Therefore

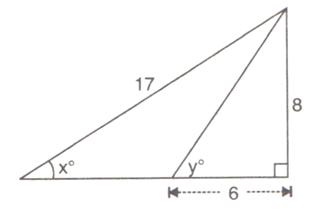
In the following figure:
AD ![]() BC, AC = 26 CD = 10, BC = 42,
BC, AC = 26 CD = 10, BC = 42,
![]() DAC = x and
DAC = x and ![]() B = y.
B = y.
Find the value of :
(i) cot x
(ii) ![]()
(iii) ![]()
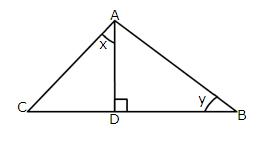
Given angle ![]() and
and ![]() in the figure
in the figure


Again

Now
(i)
![]()
(ii)
![]()
![]()
Therefore
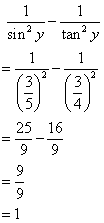
(iii)
![]()
![]()
![]()
Therefore
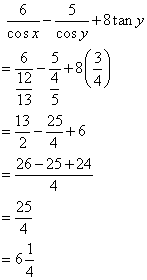
Chapter 22 - Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals] Exercise Ex. 22(B)
From the following figure, find:
(i) y (ii) sin xo
(iii) (sec xo - tan xo) (sec xo + tan xo)
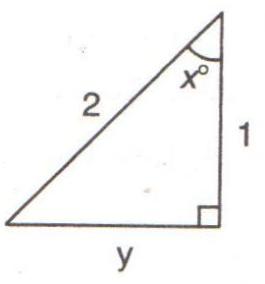
Consider the given figure

(i)
Since the triangle is a right angled triangle, so using Pythagorean Theorem
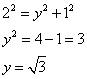
(ii)
![]()
(iii)
![]()
![]()
Therefore
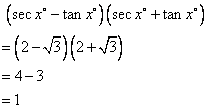
Use the given figure to find:
(i) sin xo (ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
Consider the given figure
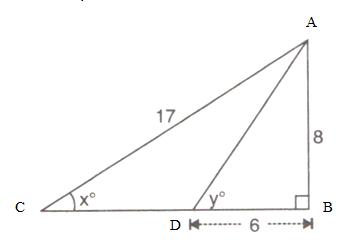
Since the triangle is a right angled triangle, so using Pythagorean Theorem
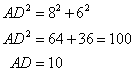
Also
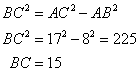
(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
![]()
Therefore
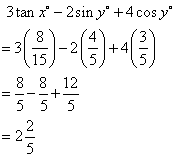
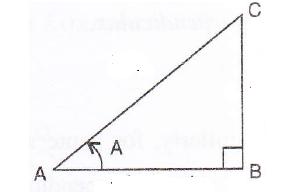
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC. Find:
(i) cos ![]() DBC (ii) cot
DBC (ii) cot ![]() DBA
DBA
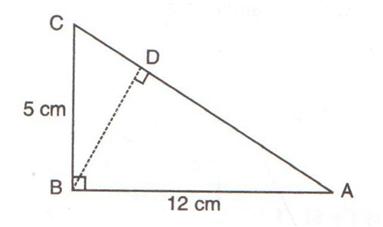
Consider the given figure

Since the triangle is a right angled triangle, so using Pythagorean Theorem

In ![]() and
and ![]() , the
, the ![]() is common to both the triangles,
is common to both the triangles, ![]() so therefore
so therefore ![]() .
.
Therefore ![]() and
and ![]() are similar triangles according to AAA Rule
are similar triangles according to AAA Rule
So

(i)
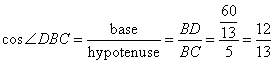
(ii)
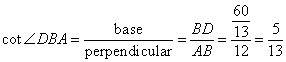
In the given figure, triangle ABC is right-angled at B. D is the foot of the perpendicular from B to AC. Given that BC = 3 cm and AB = 4 cm. find:
(i) tan ![]() DBC
DBC
(ii) sin ![]() DBA
DBA
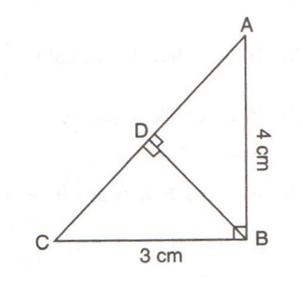
Consider the given figure

Since the triangle is a right angled triangle, so using Pythagorean Theorem
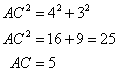
In ![]() and
and ![]() , the
, the ![]() is common to both the triangles,
is common to both the triangles, ![]() so therefore
so therefore![]() .
.
Therefore ![]() and
and ![]() are similar triangles according to AAA Rule
are similar triangles according to AAA Rule
So
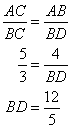
Now using Pythagorean Theorem
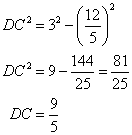
Therefore

(i)
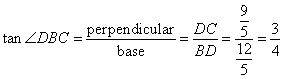
(ii)
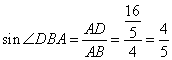
In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ![]() ABC.
ABC.
Consider the figure below
In the isosceles ![]() ,
, ![]() and
and ![]() the perpendicular drawn from angle
the perpendicular drawn from angle ![]() to the side
to the side ![]() divides the side
divides the side ![]() into two equal parts
into two equal parts ![]()
![]()
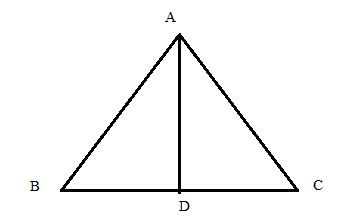
In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:
(i) sin B (ii) tan C
(iii) sin2 B + cos2B (iv) tan C - cot B
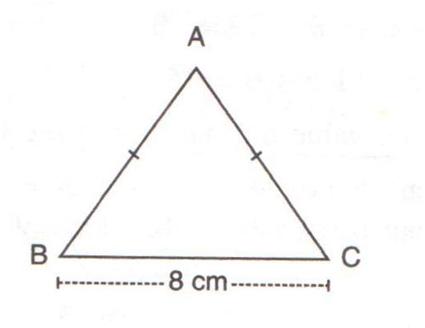
Consider the figure below
In the isosceles ![]() ,
, ![]() and
and ![]() the perpendicular drawn from angle
the perpendicular drawn from angle ![]() to the side
to the side ![]() divides the side
divides the side ![]() into two equal parts
into two equal parts ![]()
Since ![]()

(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
Therefore

(iv)
![]()
![]()
Therefore
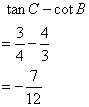
In triangle ABC; ![]() ABC = 90o,
ABC = 90o, ![]() CAB = xo, tan xo =
CAB = xo, tan xo = ![]() and BC = 15 cm. Find the measures of AB and AC.
and BC = 15 cm. Find the measures of AB and AC.
Consider the figure
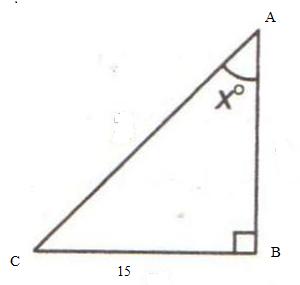

Therefore if length of base = 4x, length of perpendicular = 3x
Since
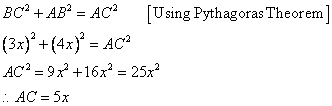
Now
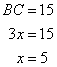
Therefore
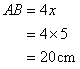
And
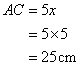
Using the measurements given in the following figure:
(i) Find the value of sin ![]() and tan
and tan![]() .
.
(ii) Write an expression for AD in terms of ![]()
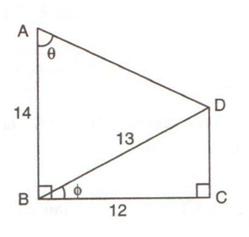
Consider the figure
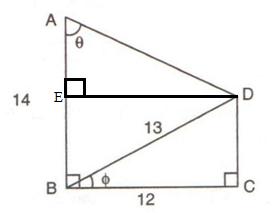
A perpendicular is drawn from D to the side AB at point E which makes BCDE is a rectangle.
Now in right angled triangle BCD using Pythagorean Theorem

Since BCDE is rectangle so ED 12 cm, EB = 5 and AE = 14 - 5 = 9
(i)
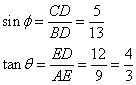
(ii)
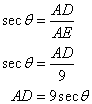
Or
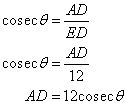
In the given figure;
BC = 15 cm and sin B =![]() .
.
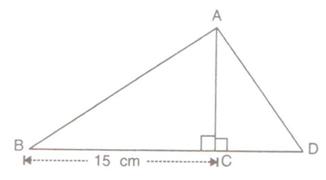
(i) Calculate the measure of AB and AC.
(ii) Now, if tan ![]() ADC = 1; calculate the measures of CD and AD.
ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - ![]()
Given
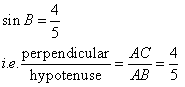
Therefore if length of perpendicular = 4x, length of hypotenuse = 5x
Since
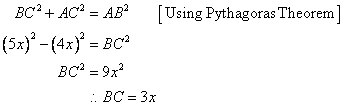
Now
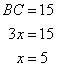
(i)
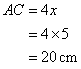
And
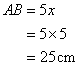
(ii)
Given
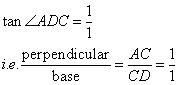
Therefore if length of perpendicular = x, length of hypotenuse = x
Since

Now
![]()
So
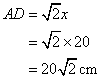
And
![]()
Now
![]()
![]()
So
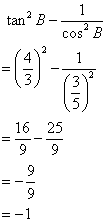
If sin A + cosec A = 2;
Find the value of sin2 A + cosec2 A.
![]()
Squaring both sides

If tan A + cot A = 5;
Find the value of tan2 A + cot2 A.
![]()
Squaring both sides

Given: 4 sin ![]() = 3 cos
= 3 cos ![]() ; find the value of:
; find the value of:
(i) sin ![]() (ii) cos
(ii) cos ![]()
(iii) cot2 ![]() - cosec2
- cosec2![]() .
.
(iv) 4 cos2![]() - 3 sin2
- 3 sin2![]() + 2
+ 2
Consider the diagram below:
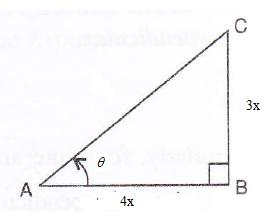

Therefore if length of BC = 3x, length of AB = 4x
Since

(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
Therefore

(iv)
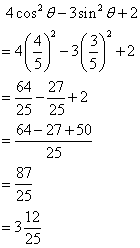
Given : 17 cos ![]() = 15;
= 15;
Find the value of: tan ![]() + 2 sec
+ 2 sec![]() .
.
Consider the diagram below:
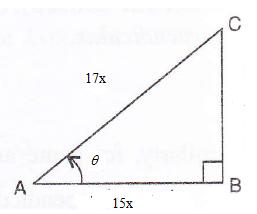
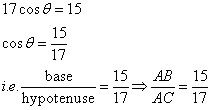
Therefore if length of AB = 15x, length of AC = 17x
Since

Now
![]()
![]()
Therefore
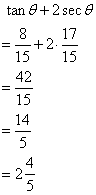
Given : 5 cos A - 12 sin A = 0; evaluate :
![]() .
.
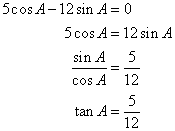
Now
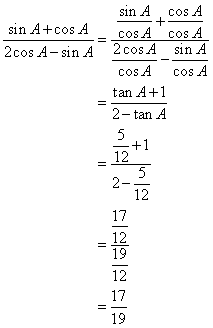
In the given figure; ![]() C = 90o and D is mid-point of AC. Find
C = 90o and D is mid-point of AC. Find
(i) ![]() (ii)
(ii) ![]()

Since ![]() is mid-point of
is mid-point of ![]() so
so ![]()
(i)
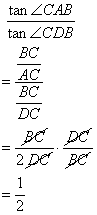
(ii)
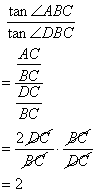
If 3 cos A = 4 sin A, find the value of :
(i) cos A(ii) 3 - cot2 A + cosec2A.
Consider the diagram below:
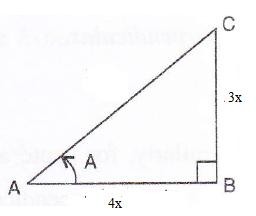
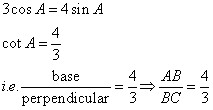
Therefore if length of AB = 4x, length of BC = 3x
Since

(i)
![]()
(ii)
![]()
Therefore
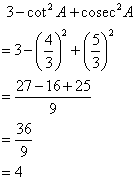
In triangle ABC, ![]() B = 90o and tan A = 0.75. If AC = 30 cm, find the lengths of AB and BC.
B = 90o and tan A = 0.75. If AC = 30 cm, find the lengths of AB and BC.
Consider the figure
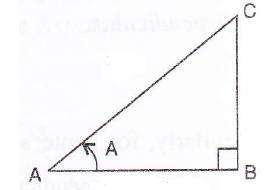
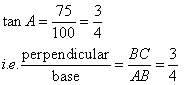
Therefore if length of base = 4x, length of perpendicular = 3x
Since
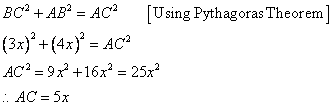
Now
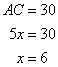
Therefore
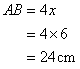
And
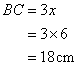
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the the side and the diagonals of the rhombus.
Consider the figure
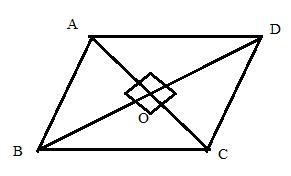
The diagonals of a rhombus bisects each other perpendicularly
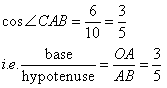
Therefore if length of base = 3x, length of hypotenuse = 5x
Since

Now
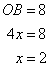
Therefore
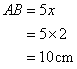
And
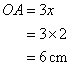
Since the sides of a rhombus are equal so the length of the side of the rhombus ![]()
The diagonals are
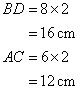
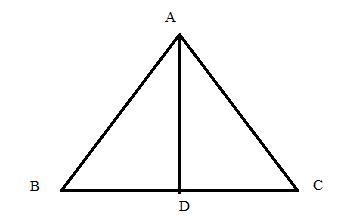
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
(i) cos B (ii) sin C
(iii) tan2 B - sec2 B + 2
Consider the figure below
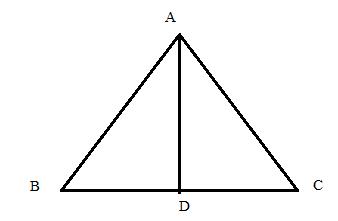
In the isosceles ![]() , the perpendicular drawn from angle
, the perpendicular drawn from angle ![]() to the side
to the side ![]() divides the side
divides the side ![]() into two equal parts
into two equal parts ![]()
Since ![]()

(i)
![]()
(ii)
![]()
(iii)
![]()
![]()
Therefore
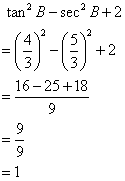
In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1. Find the length of AB, AD, AC and DC.
Consider the figure below

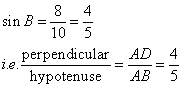
Therefore if length of perpendicular = 4x, length of hypotenuse = 5x
Since

Now
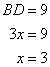
Therefore

And
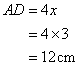
Again
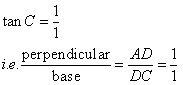
Therefore if length of perpendicular = x, length of base = x
Since

Now
![]()
Therefore
![]()
And
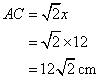
Given q tan A = p, find the value of :
![]() .
.
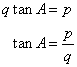
Now

If sin A = cos A, find the value of 2 tan2A - 2 sec2 A + 5.
Consider the figure

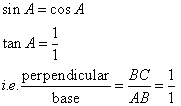
Therefore if length of perpendicular = x, length of base = x
Since

Now
![]()
Therefore

In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
Consider the diagram
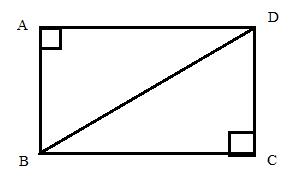
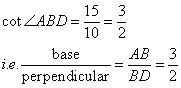
Therefore if length of base = 3x, length of perpendicular = 2x
Since

Now
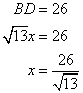
Therefore
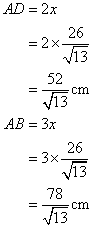
Now
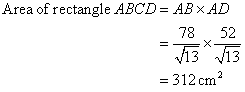

If 2 sin x = ![]() , evaluate.
, evaluate.
(i) 4 sin3 x - 3 sin x.
(ii) 3 cos x - 4 cos3 x.
Consider the figure
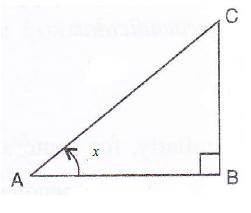
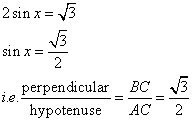
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
(i)
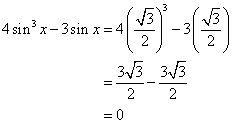
(ii)

If sin A = ![]() and cos B =
and cos B = ![]() , find the value of :
, find the value of : ![]() .
.
Consider the diagram below:
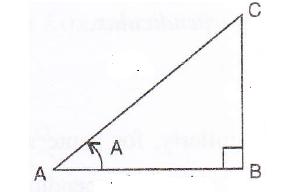

Therefore if length of ![]() , length of
, length of ![]()
Since
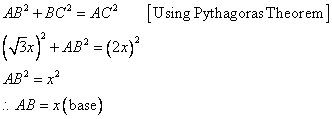
Consider the diagram below:
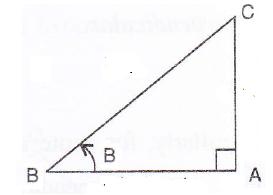
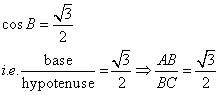
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
![]()
Therefore
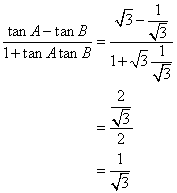
Use the informations given in the following figure to evaluate: ![]()
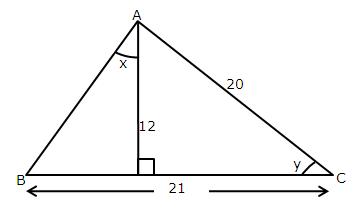
Consider the given diagram as
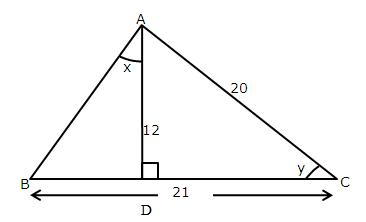
Using Pythagorean Theorem
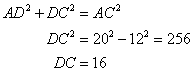
Now
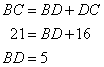
Again using Pythagorean Theorem
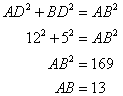
Now
![]()
![]()
![]()
Therefore
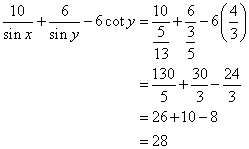
If sec A = ![]() , find:
, find: ![]() .
.
Consider the figure
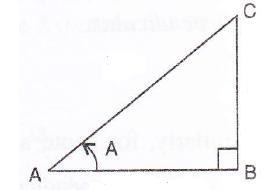
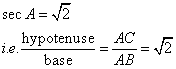
Therefore if length of ![]() , length of
, length of ![]()
Since

Now
![]()
![]()
![]()
![]()
Therefore

If 5 cos ![]() = 3, evaluate :
= 3, evaluate : ![]() .
.
![]()
Now

If cosec A + sin A = 5![]() , find the value of cosec2A + sin2A.
, find the value of cosec2A + sin2A.
![]()
Squaring both sides

If 5 cos ![]() = 6 sin
= 6 sin ![]() ; evaluate:
; evaluate:
(i) tan ![]() (ii)
(ii) ![]()
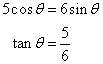
Now
(i)
![]()
(ii)
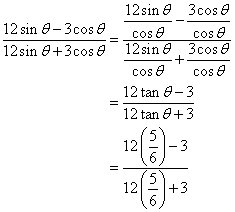
![]()
Comments
Post a Comment